| Главная » Статьи » Физика |
«Системно-функциональный подход к усвоению законов физики» Некрасова Ирина Викторовна, Индустринская ООШ I. В истории педагогических и психологических наук на протяжении многих десятилетий или даже столетий прослеживается сложная, трудноразрешимая проблема – взаимосвязь психологических и дидактических конвенций обучения и доведения их до уровня практической школьной деятельности. В дидактике нет полной ясности в категориальной принадлежности многих понятий, например, совершенно по-разному истолковываются такие понятия, как проблемное обучение, межпредметная связь и др. В одних работах их называют принципами (принцип проблемности), в других работах – методами (проблемный метод), в-третьих – подходами (проблемный подход). Это говорит о несовершенстве методологического аппарата дидактики. Если это методы, то их использование является необязательным для учителя. Если это принципы, то учитель должен следовать им неукоснительно, чтобы достичь цели урока. Если это подходы, то совершенно непонятно к чему они обязывают, т.к. понятие «подход» неопределенно теоретически в дидактике. Поэтому в последние 2 десятилетия усиленно развивается новая отрасль психолого-педагогического знания – психодидактика, - в рамках которой предложено выделить подобные психолого-педагогические понятия в качестве самостоятельной категории, назвать их методологическими подходами психодидактики и сделать предметом данной отрасли знаний. Развитию психодидактики уделяется усиленное внимание в государственных педагогических университетах: Барнаульском (проф. А.Н. Крутский) Башкирский (А.З. Рахимов) Магнитогорский (А.И. Подольский) Я строго следую авторской позиции профессора Крутского. На слайде представлены методологические подходы, среди них и системно-функциональный. Что же это такое? В чем суть подхода? Подход связан, в частности, с анализом структуры научного знания и выделением его основных частей (элементов). Из научной теории вычленены 6 ее основных элементов: (на доске) 1. Научные факты 4. Физические величины 2. Гипотезы 5. Законы 3. Идеальные объекты (модели) 6. Практическое применение теоретических знаний Каждый этот элемент имеет свои функции, однако у некоторых элементов, относящихся к разным разделам физики, эти функции повторяются. Если из различных разделов физики выбрать объекты, имеющие сходные структуры или функции, объединить их в систему и одновременно рассмотреть, то можно увидеть, что эта общность может повлечь за собой общность процедур получения знаний. Каждый из названных элементов научной теории является сложным объектом и состоит из элементов, которые зачастую имеют одинаковую структуру, несмотря на то, что могут относиться к различным разделам физики. Поэтому, разобравшись в этих структурах при изучении одной темы, можно создать и использовать общую технологию их усвоения. Это сократит объем механического запоминания, создаст условия для глубокого понимания и прочного осознания материала. Таким образом, возникает проблема создания технологий системного усвоения знаний. Вывод про величины: Знать о них надо одно и то же, и процедуры получения знаний о них одинаковы и имеют одну и ту же («общую») технологию. Переходим к системно-функциональному подходу к усвоению законов физики. Если вы зададите учащимся вопрос «Что такое физическая величина?», «Что такое закон?», то получим либо удручающий ответ, либо не получим ни какого, либо «Закон – это набор слов, который надо запомнить». Что же такое закон? Я не буду давать определение из философского словаря. Для учащихся школы функция закона как элемента знаний может быть определена следующим образом:
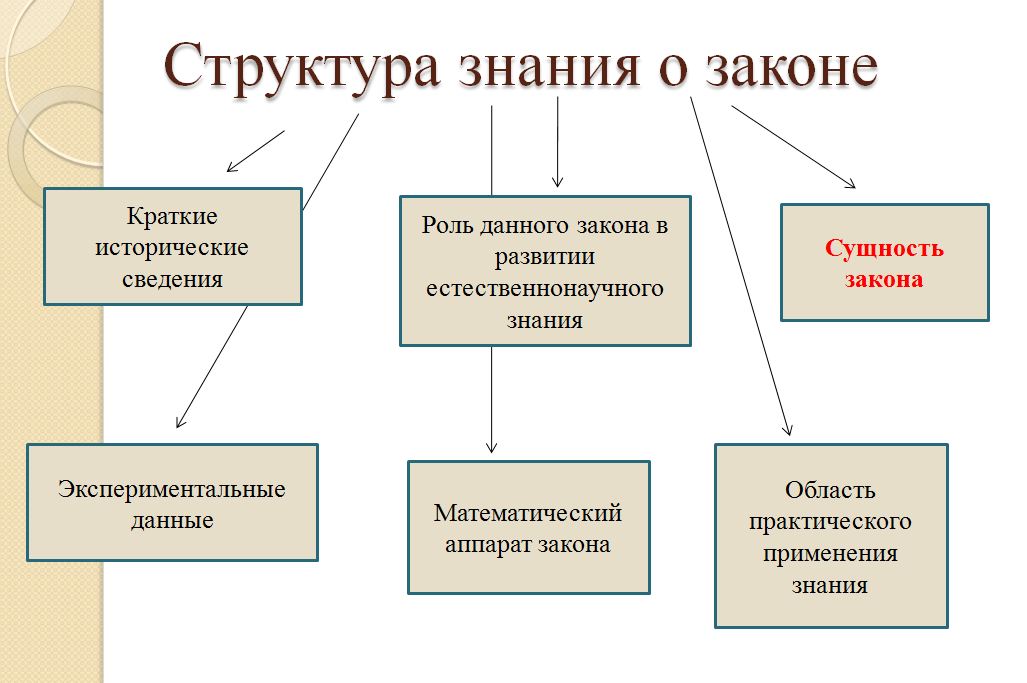
Закон – это выражение устойчивых существенных связей между физическими явлениями и характеризующими их величинами. Учащиеся должны прочно усвоить, что закон – это связь, зависимость. Эта связь должна быть устойчивой, повторяющейся. Все пункты, кроме сущности закона, не представляют особой сложности для учащихся. Их познание является лишь только результатом добросовестной учебы. Наибольшую тревогу вызывает непонимание сущности законов (даже хорошими учениками). Поэтому раскрытие именно этой части структуры знания о законе требует специальных приемов системно-функционального подхода. Большинство этих элементов знания можно получить, ничего не зазубривая по определенным технологиям, которые авторы называют «правилами системного усвоения». Законы могут выражаться в различной форме:
Рассмотрим законы, выраженные в школьных учебниках в виде формул. Среди законов есть такие, которые названы словом «закон», например, закон Ома, закон Кулона. Но есть и такие, которые не удостоились чести называться законами, хотя от этого не потеряли своей функции взаимосвязи между величинами, например, формула для сопротивления проводника . В итоге очень большое число формул названных законом, и еще больше – не названных. Сколько всего, автор предлагает выявить нам самостоятельно. Выписав и представив наглядным образом все законы, обращаем внимание на сходство внешней формы их математического выражения. Все законы физики формально могут быть выражены В левой части уравнения всегда стоит величина, значение которой определяет закон. В правой части находится коэффициент и набор переменных, от которых зависит значение величины, стоящей в левой части. При изменении любой из них меняется в соответствии с выражаемой зависимостью значение величины в левой части. Про коэффициент. По нему проще всего распознать принадлежность данной формулы к системе законов. Правда, он не всегда является обязательным компонентом. Во многих законах он равен 1. Иногда он не носит универсального характера и может быть неодинаковым в формулах одного и того же закона, например, закон Гука, закон Фарадея. В некоторых законах коэффициент пропорциональности имеет единственное значение для всех объектов. В этом случае он носит название универсальной физической константы. Правила системного усвоения. Их всего 8. (Слайд №8) I правило: Как записывать формулу? В формализованном виде это можно представить, как показано на слайде. II правило: От чего зависит величина стоящая в левой части? Говорить, что значение величины в левой части зависит от К, не следует, т.к. его значение не меняется лишь в частных случаях конкретных явлений, а в общем случае при различных ситуациях может меняться. III правило: Как зависит величина, стоящая в левой части уравнения от величин стоящих в правой части? На зависимость величины, стоящей в левой части уравнения, от коэффициента пропорциональности по ранее указанным причинам внимание не обращаем. IV правило: Ответы на 2 и 3 вопросы автоматически дают ответ на этот вопрос. Главное довести до учащихся мысль о том, что формулировки не зазубриваются, не вспоминаются, а конструируются каждый раз в соответствии с формулой. Если ученик разобрался с ответами на 2 и 3 вопросы, то он фактически уже сконструировал формулировку (см. слайд №4). В формулировках законов еще указываются условия применимости этого закона. Авторы предлагают говорить об условиях применимости говорить отдельно. Также обращают внимание на то, что законы сложны по конструкции, недоступны для понимания среднего ученика, не говоря уже о слабых. Все авторы действующих учебников, стараются в формулировку закона вложить как характер зависимости между величинами, так и условия выполнения закона, отражающие границу его применимости. Формулировку следует разделить на 2 части. В первой части целесообразно отразить характер зависимости между величинами. Во второй – уточнить характер физического процесса и указать условия и границы применимости. V правило: Как называется коэффициент пропорциональности в законе? (Это скорее не правило, а просто очередной элемент логики развития знания о законе) VI правило: Каков физический смысл коэффициента пропорциональности в законе? При выявлении физического смысла коэффициента пропорциональности, например, в законе Кулона, полезен такой прием. Закрываем в правой части формулы закона все величины кроме коэффициента. Читаем оставшуюся часть в обратную сторону: коэффициент равен силе. Когда, при каких значениях величин это будет верным? Если все они равны 1. Значит К численно равен силе с которой взаимодействуют два заряда по одному Кулону на расстоянии 1 метр. Здесь нужно говорить «численно», т.к. равны только числа коэффициента величин, но наименования их единиц различно. VII правило: Как получить наименование единицы коэффициента? Выражаем из уравнения, получаем наименование единицы коэффициента. Государственным стандартом на физические величины предусмотрены квадратные скобки, которые заменяют слова «наименование единицы физической величины» или «обозначение единицы физической величины». VIII правило: Чему равен коэффициент пропорциональности?
II. Практическая работа. (см. приложения)
III. Примеры применения методологических подходов:
IV. Список используемой литературы.
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 2
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 3741 | Рейтинг: 5.0/1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |